数学
计算机取模运算
$A % B = A - A / B * B$
结果只和左操作数有关:当左操作数为负数时,结果为负数或0;当左操作数为正数时,结果为正数或0。
两数相除
https://leetcode.cn/problems/divide-two-integers/
class Solution {
public:
int divide(const int dividend, const int divisor) {
if (dividend == INT_MIN && divisor == -1) return INT_MAX;
if (dividend == INT_MIN && divisor == 1) return INT_MIN;
if (dividend > 0) return -divide(-dividend, divisor);
if (divisor > 0) return -divide(dividend, -divisor);
// 转换为负数 / 负数,防止溢出
if (dividend > divisor) return 0;
int sub = divisor;
int result = 1;
// 防止sub + sub溢出
while (dividend - sub <= sub) {
result += result;
sub += sub;
}
return result + divide(dividend - sub, divisor);
}
};
约瑟夫环/约瑟夫问题
快速幂/快速幂取模/费马小定理
快速幂
long long fast_pow(long long base, long long idx) {
if (base == 0) return 0;
long long result = 1;
while (idx > 0) {
if (idx & 1) result *= base;
base *= base;
idx >>= 1;
}
return result;
}
快速幂取模
long long fast_pow(long long base, long long idx, long long mod) {
if (base == 0 || mod == 1) return 0;
long long result = 1;
base %= mod;
while (idx > 0) {
if (idx & 1) result = (result * base) % mod;
base = (base * base) % mod;
idx >>= 1;
}
return result;
}
费马小定理:若p为素数,gcd(a, p) = 1,则$a^{p-1} \equiv 1 \pmod p$
因此当a和p互质且p为素数时,可以计算$a^{x}\bmod p=a^{x\bmod(p-1)} \bmod p$ 来提高效率。
矩阵快速幂

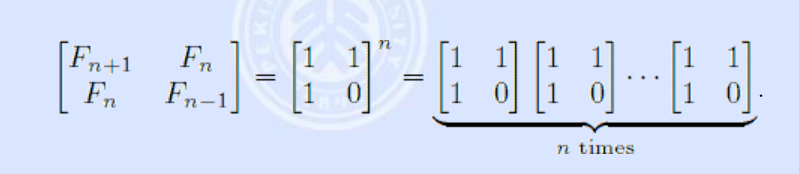
(不可用!)
//
// Created by Jiang Yinzuo on 2020/12/12.
//
#include <cstdio>
#include <cstring>
template<typename T>
struct Matrix {
int n;
T **mat;
explicit Matrix(int n) : n(n), mat(new T*[n]) {
for (int i = 0; i < n; ++i) {
mat[i] = new T[n];
}
}
~Matrix() {
for (int i = 0; i < n; ++i) {
delete []mat[i];
}
delete[] mat;
}
Matrix operator*(const Matrix &m) {
Matrix<T> res(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
res.mat[i][j] = 0;
for (int k = 0; k < n; ++k) {
res.mat[i][j] += mat[i][k] * m.mat[k][j];
}
}
}
return res;
}
Matrix operator%=(T mod) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
mat[i][j] %= mod;
}
}
return *this;
}
Matrix pow(T idx) {
Matrix<T> ans(n);
memset(ans, 0, sizeof(ans));
Matrix<T> base(n);
for (int i = 0; i < n; ++i) {
ans.mat[i][i] = 1;
}
while (idx) {
if (idx & 1) {
ans = ans * base;
}
base = base * base;
idx >>= 1;
}
return ans;
}
Matrix pow(T idx, T mod) {
Matrix<T> ans(this->n);
Matrix<T> base = *this;
for (int i = 0; i < n; ++i) {
ans.mat[i][i] = 1;
}
while (idx) {
if (idx & 1) {
ans = ans * base;
ans %= mod;
}
base = base * base;
base %= mod;
idx >>= 1;
}
return ans;
}
};
int main() {
int n, k;
scanf("%d %d", &n, &k);
Matrix<int> base(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d", &base.mat[i][j]);
}
}
auto ans = base.pow(k, 1000000007);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
printf("%d ", ans.mat[i][j]);
}
puts("");
}
return 0;
}
组合数学
组合数打表
$\mathrm C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$
long long C[1009][1009];
constexpr long long MOD = 1e9 + 7;
void init() {
for (int n = 0; n <= 1003; ++n) {
C[n][0] = C[n][n] = 1;
for (int m = 1; m < n; ++m) {
C[n][m] = (C[n - 1][m] + C[n - 1][m - 1]) % MOD;
}
}
}
只算少数几个组合数
阶乘打表,$$C_n^m = \frac{n!}{(n-m)!m!}$$
公式
平方和公式$$\sum \limits_{i=1}^n = n(n+1)(2n+1)/6$$
常数
PI = 3.14159265358979323846